Problem Setup

The Variational Lower Bound is also knowd as Evidence Lower Bound(ELBO) or VLB. It is quite useful that we can derive a lower bound of a model containing a hidden variable. Futhermore, we can even maximize the bound to maximize the log probability. We can assume that $X$ are observations (data) and $Z$ are hidden/latent variables which is unobservable. In general, we can also imagine $Z$ as a parameter and the relationship between $Z$ and $X$ are represented as the following

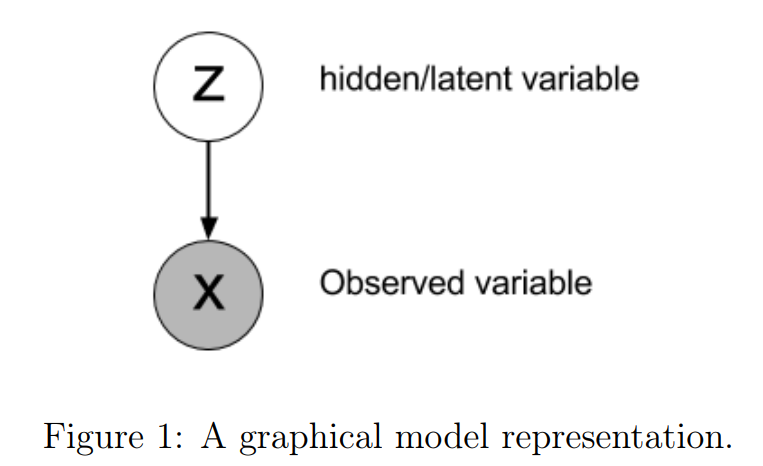
In the mean time, by the definition of Bayes’ Theorem and conditional probability, we can get

$$p(Z | X) = \frac{p(X | Z) p(Z)}{p(X)} = \frac{p(X | Z) p(Z)}{\int_{Z} p(X, Z)}$$

Jensen’s Inequality

It states that for the convex transformation $f$, the mean $f(w \cdot x + (1 - w) y)$ of $x$, $y$ on convex transform $f$ is less than or equal to the mean applied after convex transformation $w \cdot f(x) + (1 - w) f(y)$.

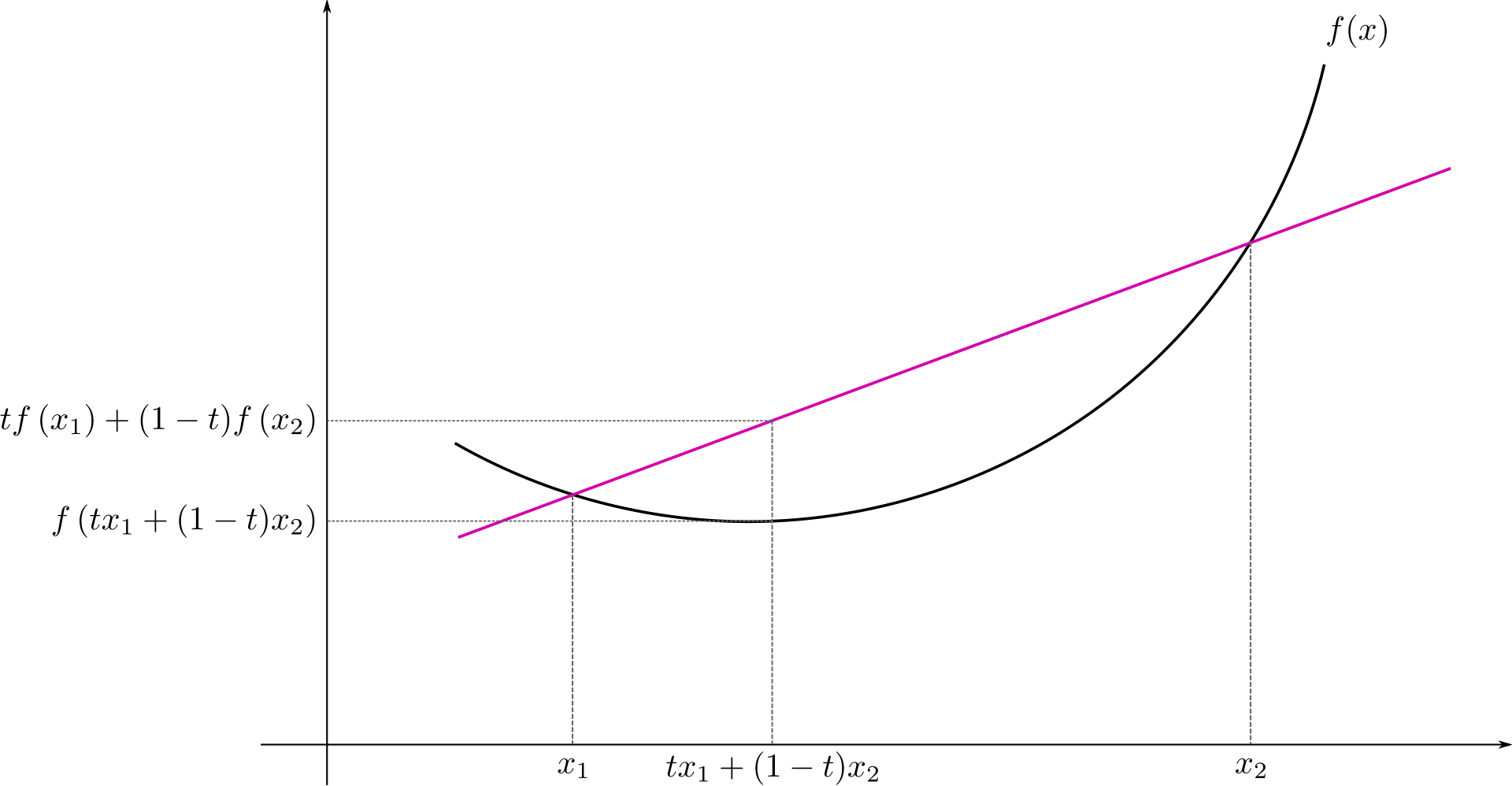
Formaly, corresponding to the notation of the above figure, the Jensen’s inequality can be defined as

$$f(t x_1 + (1 - t) x_2) \leq t f(x_1) + (1 - t) f(x_2)$$

In probability theory, for a random variable $X$ and a convex function $\varphi$, we can state the inequality as

$$\varphi \ (E[X]) \leq E[\varphi(X)]$$

Proof

By the above statement, we can derive

$$ log \ p(X) = log (\int_Z \ p(X, Z)) $$

$$ = log \int_Z \ p(X, Z) \frac{q(Z)}{q(Z)} \tag{2} $$

$$ = log \int_Z \ q(Z) \frac{p(X, Z)}{q(Z)} $$

$$ = log ( E_q[\frac{p(X, Z)}{q(Z)}] ) $$

$$ \geq E_q[log \ \frac{p(X, Z)}{q(Z)}] \tag{4} $$

$$ = E_q[log \ p(X, Z) - log \ q(Z)] $$

$$ = E_q[log \ p(X, Z)] - E_q[log \ q(Z)] $$

$$ = E_q[log \ p(X, Z)] + H[Z] \tag{5} $$

Where $q(Z)$ in Eq. (2) is the approximation of the true posterior distribution $p(Z|X)$, since we don’t know the distribution of the $p(Z|X)$ of hidden state $Z$. To derive the lower bound, we apply Jensen’s inequality in Eq. (4).

Also, the Eq. (5) is the ELBO.

Then, we denote L as ELBO as following

$$ L = E_q[log \ p(X, Z)] + H[Z] $$

So far, we’ve know what’s the ELBO. The accuracy of ELBO is depend on the accuracy of the approximation of $q(Z) \approx p(Z|X)$. If we could get a better approximation, the lower bound would be more accurate. To quantify the accuracy of the approximation, we need to do something more.

Derive With KL-Divergence

Since KL-divergence is a common metric to measure the distance between distributions and $q(Z)$ is an approximation of $p(Z|X)$, the KL-Divergence between $q(Z)$ and $p(Z|X) \geq 0$. We can further derive:

$$ KL[q(Z) || p(Z|X)] = \int_Z q(Z) \ log \ \frac{q(Z)}{p(Z|X)} $$

$$ = - \int_Z q(Z) \ log \ \frac{p(Z|X)}{q(Z)} $$

$$ = - \int_Z q(Z) \ log \ \frac{p(Z, X)}{q(Z) p(X)} $$

$$ = - \int_Z q(Z) \ (log \ \frac{p(Z, X)}{q(Z)} - log \ p(X)) $$

$$ = - \int_Z q(Z) \ log \ \frac{p(Z, X)}{q(Z)} + \int_Z q(Z) \ log \ p(X) $$

$$ = E_q[log \ \frac{p(X, Z)}{q(Z)}] + log \ p(X) \int_Z q(Z) $$

$$ = -L + log \ p(X) $$

Then we rearrange the equation

$$ L = log \ p(X) - KL[q(Z) || p(Z|X)] $$

Again, $L$ is the ELBO.

The Application of ELBO

We can maximize the $log \ p(X)$ with ELBO. With KKT, we can rewrite the optimization of log probability of $X$

$$\mathop{\max}(log \ p(X))$$

to

$$\mathop{max}(log \ p(X) - \beta KL[q(Z)||p(Z|X)])$$

Thus, we can optimize the model containing hidden variable with known $p(X), p(Z|X)$ and the approximation of the hidden variable $q(Z)$. It’s a very useful trick in the model-based RL.

For more detail, please refer to this handout and wikipedia. They’ve given a great explaination. If you understand Chinese, you can read this blog. The author gives a series of blogs discussing about it.