Introduciton

Propose an efficient method for online adaptation. The algorithm efficiently trains a global model that is capable of using its recent experiences to quickly adapt, achieving fast online adaptation in dynamic environments.

They evaluate 2 version of approaches on stochastic continuous control tasks:

(1) Recurrence-Based Adaptive Learner (ReBAL)

(2) Gradient-Based Adaptive Learner (GrBAL)

Objective Setting-Up

To adapt the dynamic environment, we require a learned model $p_{\theta}^$ to adapt, using an update rule $u_{\psi}^$ after seeing M data points from some new “task”. In other words, we aim to train a global (world) model which is trained on to simulate the original environment to adapt a new environment rapidly.

Also, We assume a distribution of environments $\rho(\varepsilon)$ that share some common structure between original enironment and the new environment, such as the same observation and action space, but may differ in their dynamics $p_{\varepsilon} (s’|s, a)$.

A sequence of states and actions is denoted by $\tau_{\varepsilon} (i, j) = (s_i, a_i, …, s_j , a_j , s_{j+1})$.

The likelihood of the data under a predictive model pˆθ’ (s’|s, a) with parameters $\theta’$, where $\theta’ = u_{\psi}(\tau_{\varepsilon} (t − M, t − 1), \theta)$ corresponds to model parameters that were updated using the past $M$ data points($u_{\psi}$ is the update rule of the predictive model).

Then we formulate the optimization problem as the following

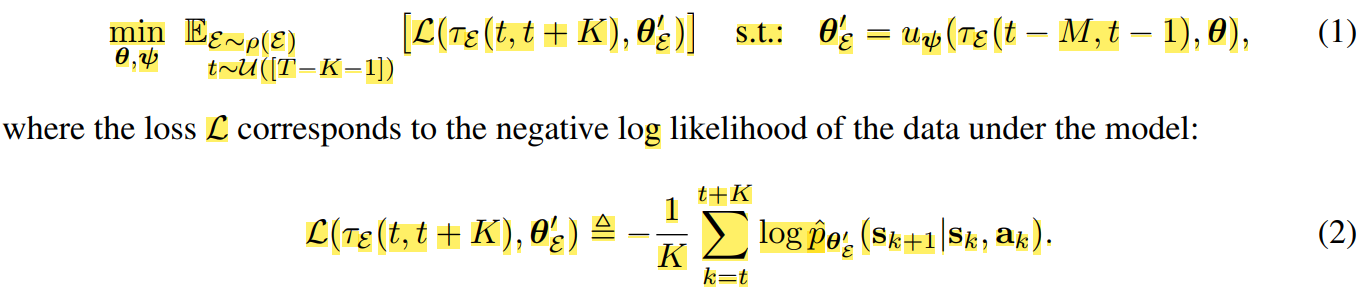
Note that the past $M$ points are used to adapt $\theta$ into $\theta’$, and the loss of this $\theta’$ is evaluated on the future $K$ points. Thus, we use the past M timesteps to provide insight into how to adapt our model to perform well for nearby future timesteps

Then we can define 2 kinds of algorithm to update the model

(1) Gradient-Based Adaptive Learner (GrBAL)

GrBAL uses a gradient-based meta-learning to perform online adaptation; in particular, we use MAML.

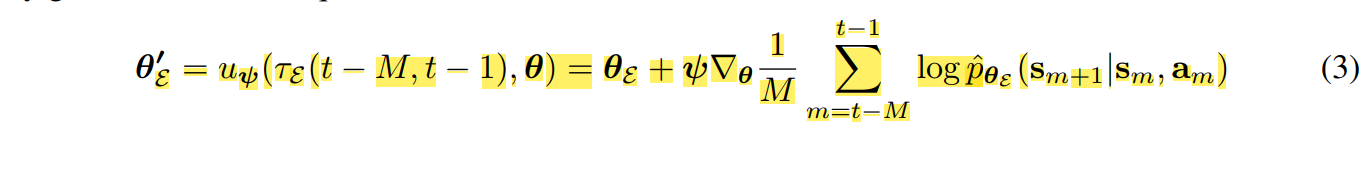
(2) Recurrence-Based Adaptive Learner (ReBAL)

ReBAL, instead, utilizes a recurrent model, which learns its own update rule (i.e., through its internal gating structure. In this case, $\psi$ and $u_{\psi}$ corresponds to the weights of the recurrent model that update its hidden state.

Algorithm

The model adaptation approach is agnostic to the model predictive control (MPC) method used. For more detail of MPC, refer to this.

Here we denote the reward function as $r$ and a planning horizon as $H$.