Shannon Entropy

For discrete random variable $X$ with events $\{ x_1, …, x_n \}$ and probability mass function $P(X)$, we defien the Shannon Entropy $H(X)$ as

$$H(X) = E[-log_b \ P(X)] = - \sum_{i = 1}^{i = n} \ P(x_i) log_b \ P(x_i)$$

where $b$ is the base of the logarithm. The unit of Shannon entropy is bit for $b = 2$ while nat for $b = e$

The Perspective of Venn Diagram

We can illustrate the relation between joint entropy, conditional entropy, and mutual entropy as the following figure

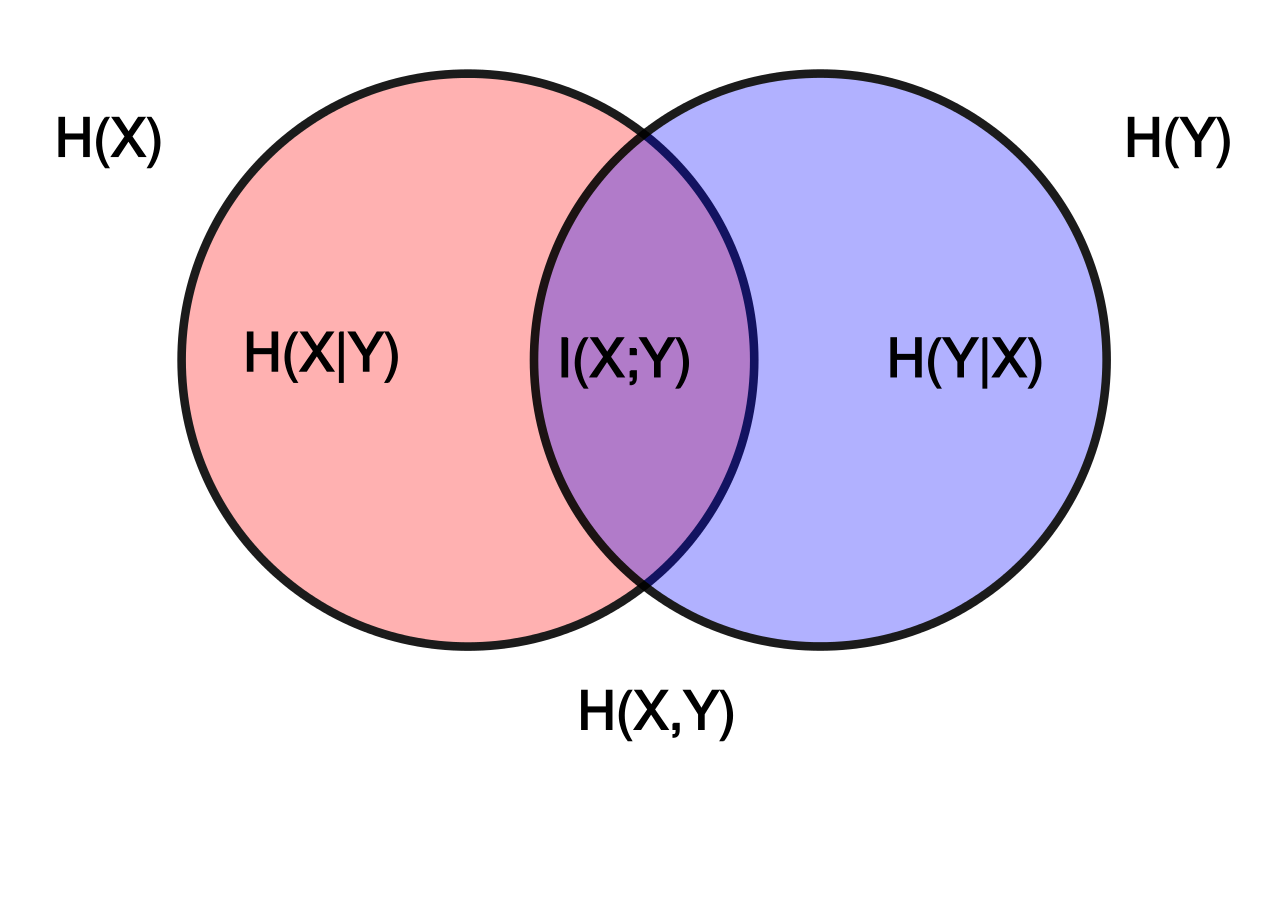
where $H(X), \ H(Y)$ are Shannon entropy of RV $X, \ Y$ respectively. $H(X, Y)$ is the joint entopy. $I(X; Y)$ is the mutual entropy. $H(X|Y), \ H(Y|X)$ are conditional entropy that given $Y$ and $X$ respectively.

Joint Entropy

The joint distribution is $P(X,Y)$ for two discrete random variables $X$ and $Y$. Thus the joint entropy is defined as

$$H(X, Y) = E[-log \ P(X, Y)] = - \sum_{i = 1}^{i = n} \sum_{j = 1}^{j = n} \ P(x_i, y_j) log \ P(x_i, y_j)$$

Conditional Entropy

The conditional entropy of $Y$ given $X$ is defined as

$$H(Y | X) = H(X, Y) - H(Y)$$

$$= - \sum_{i = 1}^{i = n} \sum_{j = 1}^{j = n} \ P(x_i, y_j) log \ P(x_i, y_j) - (- \sum_{j = 1}^{j = n} \ P(y_j) log \ P(y_j))$$

$$= \sum_{j = 1}^{j = n} \ (\sum_{i = 1}^{i = n} P(x_i, y_j)) log \ (\sum_{i = 1}^{i = n} P(x_i, y_j)) - \sum_{i = 1}^{i = n} \sum_{j = 1}^{j = n} \ P(x_i, y_j) log \ P(x_i, y_j)$$

$$ = \sum_{i = 1}^{i = n} \sum_{j = 1}^{j = n} \ P(x_i, y_j) (log \ (\sum_{i = 1}^{i = n} P(x_i, y_j)) - log \ P(x_i, y_j)) $$

$$ = \sum_{i = 1}^{i = n} \sum_{j = 1}^{j = n} \ P(x_i, y_j) (- log \ \frac{P(x_i, y_j)}{P(y_j)}) $$

$$ = - \sum_{i = 1}^{i = n} \sum_{j = 1}^{j = n} \ P(x_i, y_j) log \ \frac{P(x_i, y_j)}{P(y_j)} $$

Mutual Information(MI)

In general, MI is the intersection or say the common information for both random variables $X$ and $Y$.

Let $(X,Y)$ be a pair of random variables with values over the space $X \times Y$. If their joint distribution is $P(X,Y)$ and the marginal distributions are $P_X(X)$ and $P_Y(Y)$, the mutual information is defined as

$$I(X; Y) = H(X) + H(Y) - H(X, Y)$$

$$ = - \sum_{i = 1}^{i = n} \ P_X(x_i) log \ P_X(x_i) - \sum_{j = 1}^{j = n} \ P_Y(y_j) log \ P_Y(y_j) + \sum_{i = 1}^{i = n} \sum_{j = 1}^{j = n} \ P(x_i, y_j) log \ P(x_i, y_j) $$

$$ = - \sum_{i = 1}^{i = n} \ (\sum_{j = 1}^{j = n} P(x_i, y_j)) \ log (\sum_{j = 1}^{j = n} P(x_i, y_j)) - \sum_{j = 1}^{j = n} \ (\sum_{i = 1}^{i = n} P(x_i, y_j)) \ log (\sum_{i = 1}^{i = n} P(x_i, y_j)) $$

$$ +\sum_{i = 1}^{i = n} \sum_{j = 1}^{j = n} \ P(x_i, y_j) log \ P(x_i, y_j) $$

$$ = \sum_{i = 1}^{i = n} \sum_{j = 1}^{j = n} \ P(x_i, y_j) log \ \frac{P(x_i, y_j)}{P_X(X) \ P_Y(Y)} $$

In the view of set, MI can also be defined as

$$I(X; Y) = H(X) + H(Y) - H(X, Y)$$

$$ = H(X) - H(X | Y) = H(Y) - H(Y | X) $$

$$ = H(X, Y) - H(X | Y) - H(Y | X) $$