Multi-Armed Bandit Problem
Imagine you are in a casionoand face multiple slot machines. Each machine is configured with an unknown probability of how likely you would get a reward at one play. The question is What’s the strategy to get the highest long-term reward?
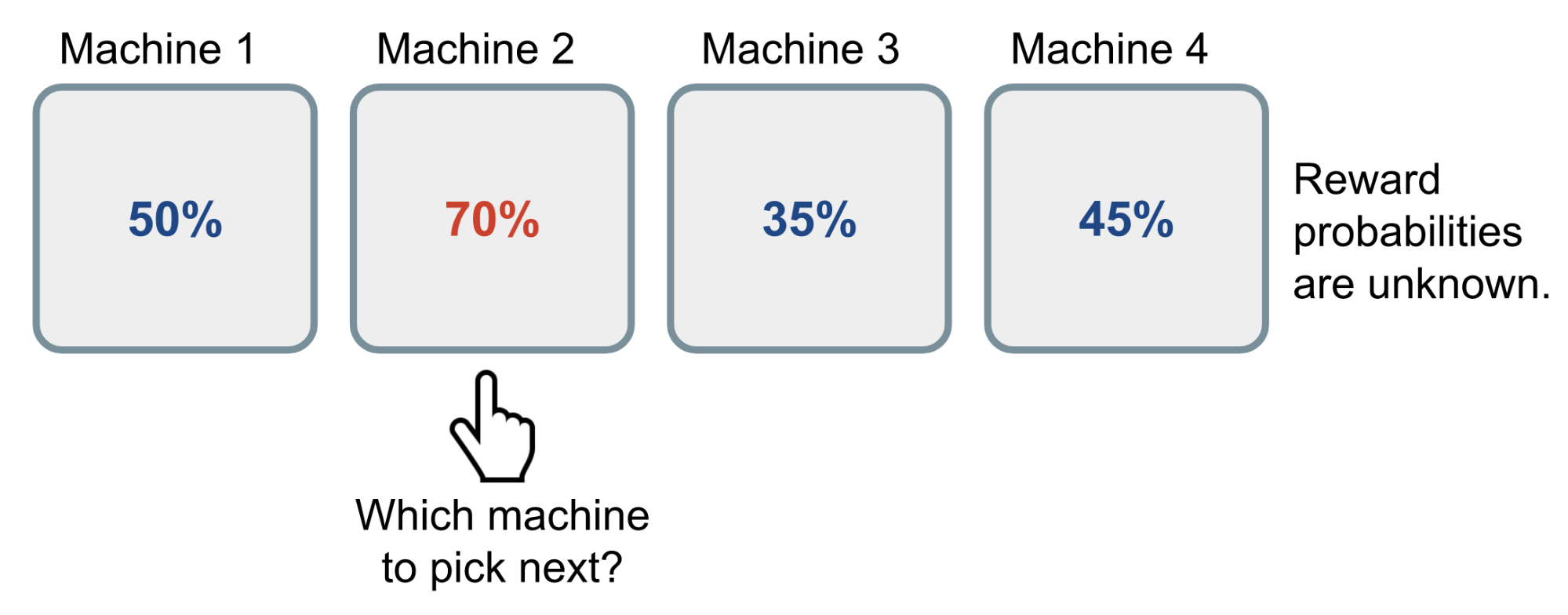An illustration of multi-armed bandit problem, refer to Lil’Log The Multi-Armed Bandit Problem and Its Solutions
Definition
Upper Confidence Bounds(UCB)
The UCB algorithm give a realtion between upper bound and probability confidence. That is to say, the UCB gives How likely is the real value of a random variable below the upper bound? To achieve this goal, we need to understand Hoeffding’s Inequality first.
Hoeffding’s Inequality
Let $X_1,…,X_t$ be i.i.d. (independent and identically distributed) random variables and they are all bounded by the interval $[0, 1]$. The sample mean is
$\overline{X}_t = \frac{1}{t} \sum_{\tau=1}^t X_\tau$
Then for $u > 0$, we have:
$$ P( E[X] > \overline{X}_t + u) \leq e^{-2tu^2} $$
The inequation gives an upper bound in probability. Once the probability is small enough, we can say the upper bound is correct almost surely.
Combine the Hoeffding’s Inequality and our goal. We can dervie
$$ P( Q(a) > \hat{Q}_t(a) + U_t(a)) \leq e^{-2t{U_t(a)}^2} $$
Once we get the bound, we can specify a target confidnce and always choose the action having highest upper bound.
$$ a^{UCB}t = argmax{a \in \mathcal{A}} \hat{Q}_t(a) + \hat{U}_t(a) $$
UCB1 Algorithm
Since we want to measure the confidence of the upper bound, we can derive the confidence with the times of acting.
$$ U_t(a) = \sqrt{\frac{2 \log t}{N_t(a)}} \text{ and } a^{UCB1}t = \arg\max{a \in \mathcal{A}} Q(a) + \sqrt{\frac{2 \log t}{N_t(a)}} $$