Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model
It is just the paper proposing MuZero. MuZero is quite famous when I write this note(Jan 2021). Lots of people tried to reproduce the incredible performance of the paper. Some of well-known implementations like muzero-general give a clear and modular implementation of MuZero. If you are interested in MuZero, you can play with it. Well, let’s diving into the paper.
Introdution
The main idea of MuZero is to predict the future that are directly relevant for planning. The model receives the observation (e.g. an image of the Go board or the Atari screen) as an input and transforms it into a hidden state. The hidden state is then updated iteratively by a recurrent process that receives the previous hidden state and a hypothetical next action. At every one of these steps the model predicts the policy (e.g. the move to play), value function (e.g. the predicted winner), and immediate reward (e.g. the points scored by playing a move).
Algorithm

Components
The MuZero consist of 3 components: dynamic function, prediction function, representation function:
Dynamic Function $g(s^t, a^{t+1})=r^{t+1}, s^{t+1}$
Prediction Function $f(s^t)=p^t, v^t$
Representation Function $h(o^0)=s^0$
We denote $o^0$ as the initial observation, $s^0$ as the initial hidden state, $p^t$ as the policy function, $v^t$ as value function, and $r^t$ as reward function at time step $t$. These 3 components compose the deterministic latent dynamic model for MuZero. (The paper says stochastic transitions is left for future works)
The MuZero plan like Figure1 part A. Given a previous hidden state $s^{k−1}$ and a candidate action $a^k$, the dynamics function $g$ produces an immediate reward $r^k$ and a new hidden state $s^k$. The policy $p^k$ and value function $v^k$ are computed from the hidden state $s^k$ by a prediction function $f$.
Acting
The MuZero act in the environment like part B of Figure1. A Monte-Carlo Tree Search is performed at each timestep $t$, as described in A. An action $a_{t+1}$ is sampled from the search policy $\pi_t$. The environment receives the action and generates a new observation $o_{t+1}$ and reward $u_{t+1}$. At the end of the episode the trajectory data is stored into a replay buffer.
The MuZero model $\mu_{\theta}$ with parameters $\theta$, conditioned on past observations $o_1, …, o_t$ and future actions $a_{t+1}, …, a_{t+k}$.
The model always predicts the policy $p_t^k$, value function $v_t^k$, and immdiate reward $r_t^k$ after $k$ time steps at timestep $t$. For more detailed, the three future quantities are as following:
Policy
$$ p_t^k \approx \pi (a_{t+k+1} | o_{1}, …, o_t, a_{t+1}, …, a_{t+k}) $$
where $\pi$ is the policy used to select real actions
Value Function
$$ v_t^k \approx E[u_{t+k+1} + \gamma \ u_{t+k+2} + … | o_1 , …, o_t, a_{t+1}, …, a_{t+k}] $$
where $u$ is the true, observation reward. $\gamma$ is the discount factor of the environment.
Immediate Reward
$$ r_t^k \approx u_{t + k} $$
Training
The MuZero train in the environment like part C of Figure1.
All parameters of the model are trained jointly to accurately match the policy, value, and reward, for every hypothetical step $k$, to corresponding target values observed after $k$ actual time-steps t have elapsed.(That is predict the policy, value, and reward after $k$ steps from current time-step $t$.) The training objective is to minimise the error between predicted policy $p_t^k$ and MCTS search policy $\pi_{t+k}$.
For trade-off between accuracy and stability, we allow for long episodes with discounting and intermediate rewards by bootstrapping $n$ steps into the future from the search value. Final outcomes {lose, draw, win} in board games are treated as rewards $u_t \in \{ −1, 0, +1 \}$ occurring at the final step of the episode.
Thus, MuZero define $z_t$ as folowing:
$$ z_t = u_{t+1} + \gamma u_{t+2} + … + \gamma^{n-1} u_{t+n} + \gamma^n u_{t+n} $$
Then, the loss function of MuZero is
$$ l_t(\theta) = \sum_{k=0}^K l^{p}(\pi_{t+k}, p_t^k) + \sum_{k=0}^K l^v(z_{t+k}, v_t^k) + \sum_{k=1}^K l^r(u_{t+k}, r_t^k) + c ||\theta||^2 $$
where $l^p$, $l^v$ and $l^r$ are loss functions for policy, value and reward, respectively. $c$ is a L2 regularization constant.
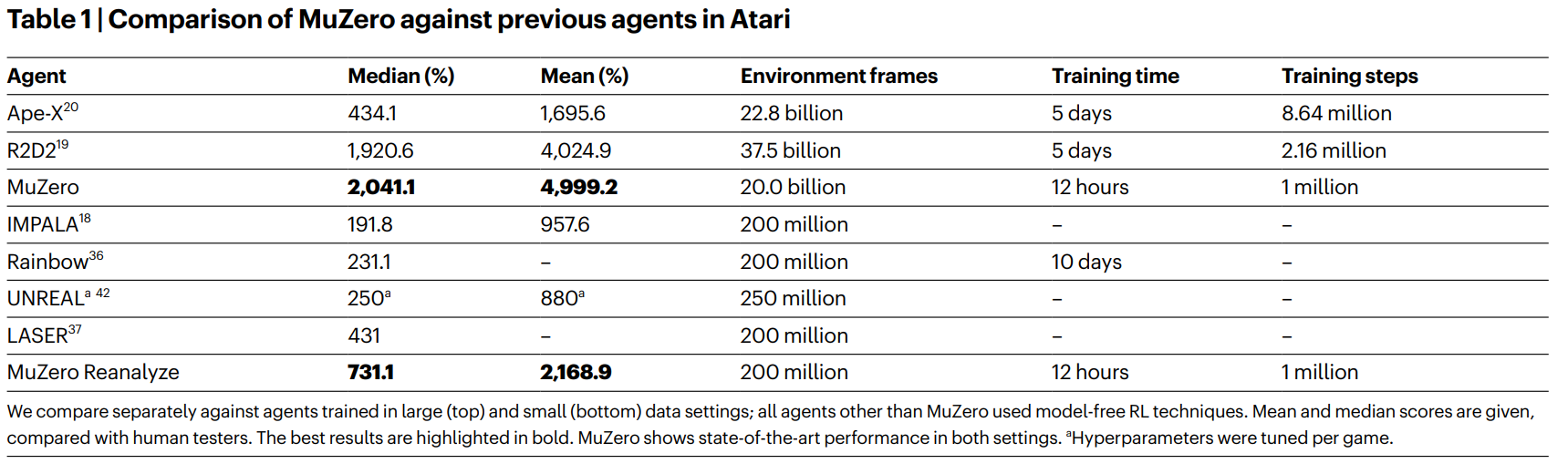
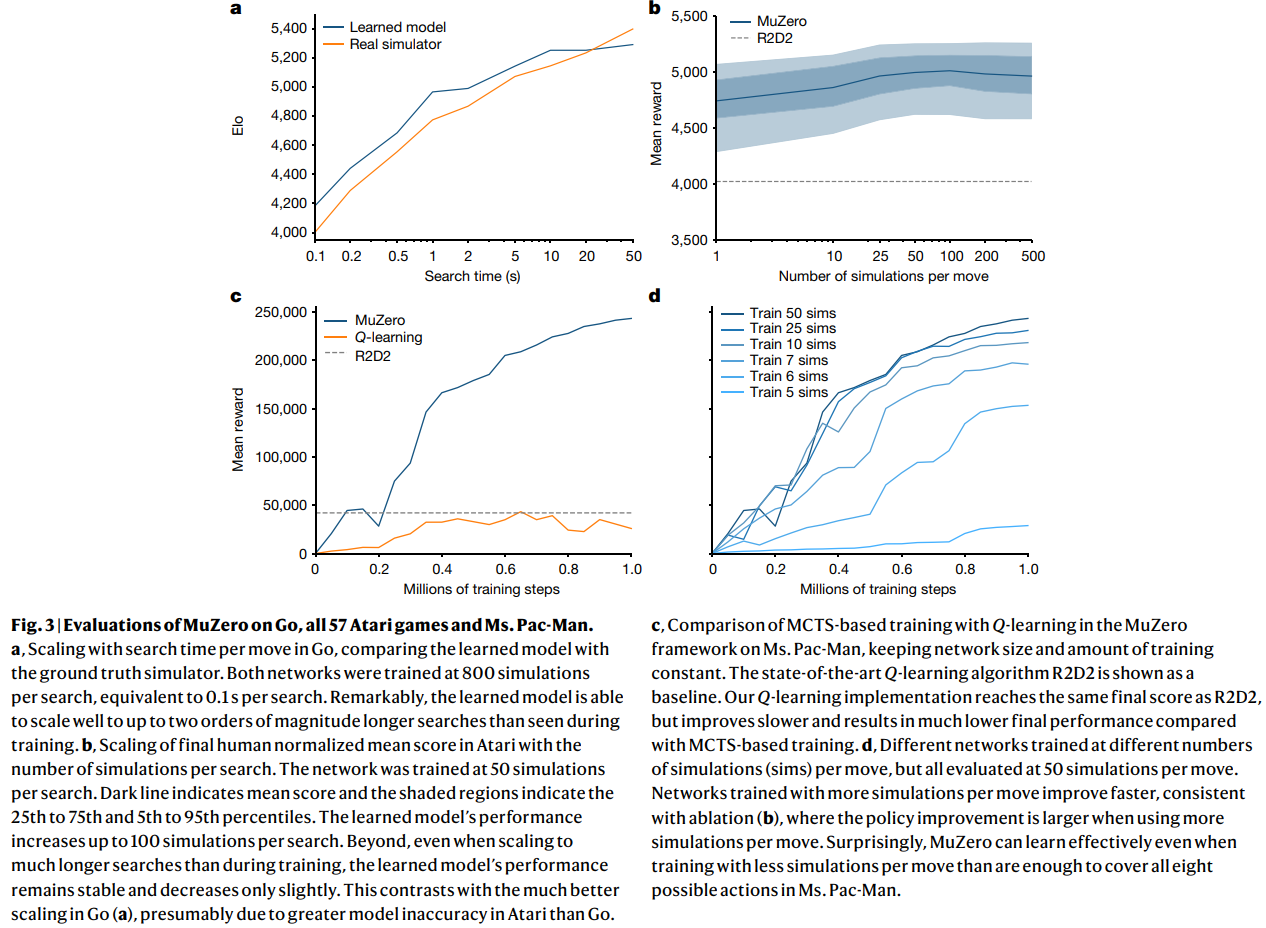
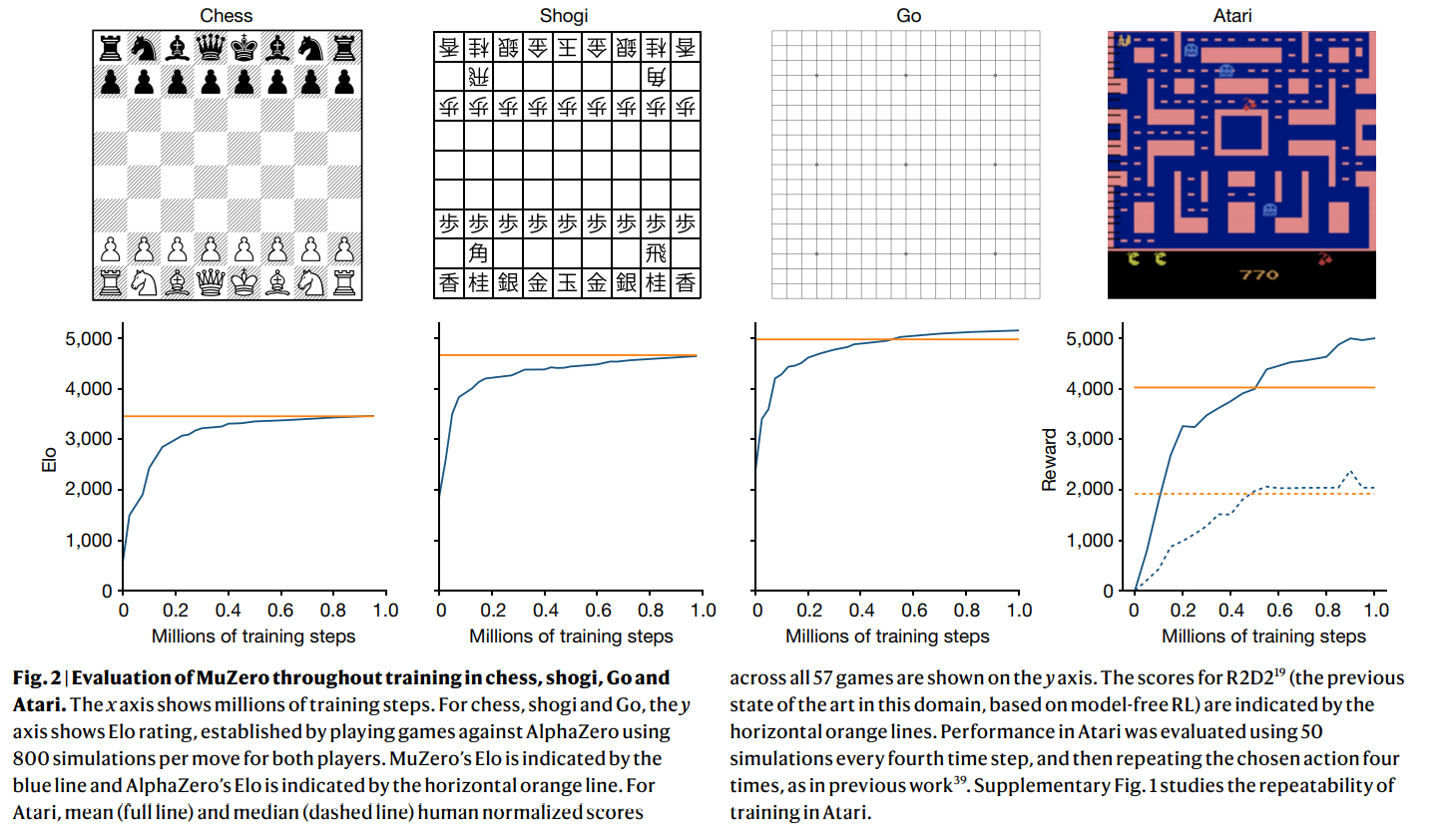
Experiments & Results
MuZero performs quite well both on board game and Atari 57.
Board Game
Atari 57