Value-Decomposition Network(VDN)
QMIX
Problem Setup And Assumption
Constraint
The QMIX imporve the VDN algorithm via give a more general form of the contraint. It defines the contraint like
$$\frac{\partial Q_{tot}}{\partial Q_{a}} \geq 0, \forall a$$
where $Q_{tot}$ is the joint value function and $Q_{a}$ is the value function for each agent.
An intuitive eplaination is that we want the weights of any individual value function $Q_{a}$ are positive. If the weights of individual value function $Q_{a}$ are negative, it will discourage the agent to cooperate, since the higher $Q_{a}$, the lower joint value $Q_{tot}$. Trivially, the contraint of VDN is just a special case that $\frac{\partial Q_{tot}}{\partial Q_{a}} = 1$.
Network Architecture
The architecture of QMIX is like the following figure
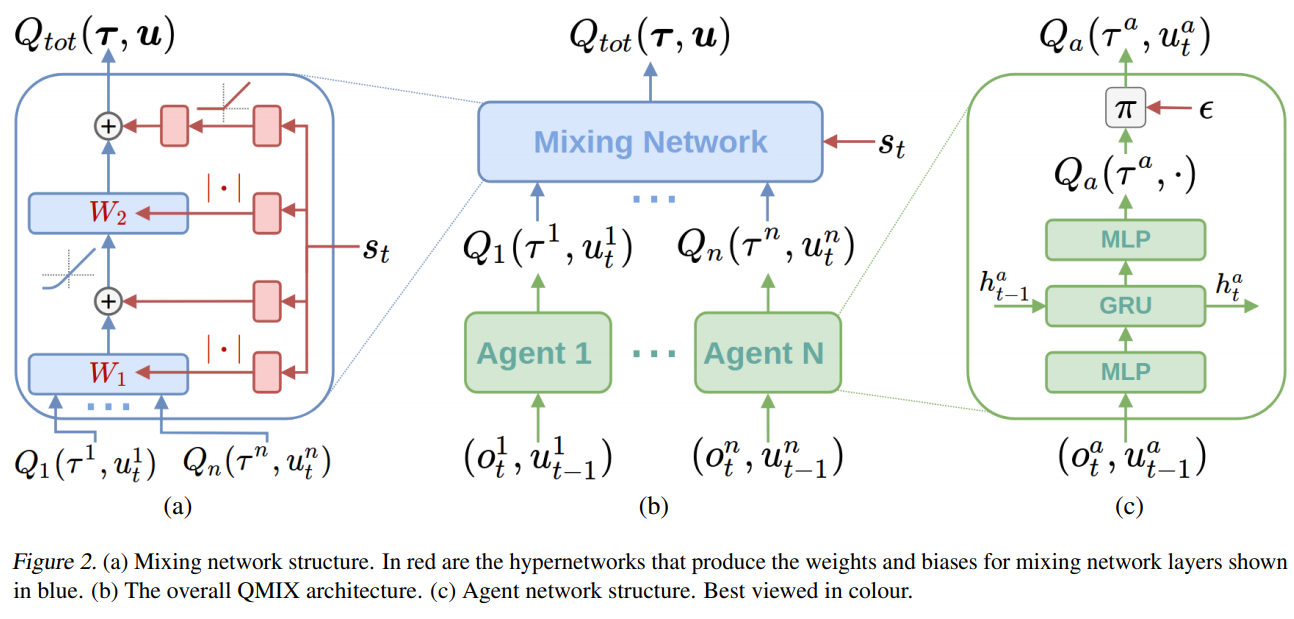
For each agent a and time step $t$, there is one agent network that represents its individual value function $Q_a(τ^a, u_t^a)$. We represent agent networks as DRQNs that receive the current individual observation $o_t^a$and the last action $u_{t−1}^a$ as input at each time step.
The mixing network is a feed-forward neural network that takes the agent network outputs $Q_a(τ^a, u_t^a)$ as input and mixes them monotonically, producing the values of $Q_{tot}$. To enforce the monotonicity constraint, the weights (but not the biases) of the mixing network are restricted to be non-negative and is produced by hypernetwork.
Each hypernetwork consists of a single linear layer, followed by ReLU function to ensure that the mixing network weights are non-negative. Since we’ve assume that the multi-agent probllem can be solve by a joint value function. The hypernetworks take the current state $s_t$ as input.
Loss Function
QMIX can be trained end-by-end, the loss function is defined as
$$L(\theta) = \sum_{i = 1}^{b}[(y_i^{tot} - Q_{tot}(\tau, u, s; \theta))^2]$$
where $b$ is the batch size of transitions sampled from the replay buffer, and $y_{tot} = r + \gamma \ max_{u’} \ Q_{tot}(τ’, u’, s’; θ^−)$, and $θ^-$ are the parameters of a target network asin DQN
Weighted QMIX
Papers
IQL
Stabilising Experience Replay for Deep Multi-Agent Reinforcement Learning
VDN
Value-Decomposition Networks For Cooperative Multi-Agent Learning
QMIX
QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning
Weighted QMIX
